|
熱酸化膜の形成が、ウエハーの粗さにどのように関係しているかを知ることは興味深いテーマである。研磨したシリコンウエハーの典型的な粗さは2nm前後(P-V)である。不規則な粗さの集合はしばしばステップ、テラスなどと呼ばれる高次構造を形成する。これらのスケールファクターは100nm程度である。成膜は熱的過程なのでエントロピーを増大させ、よってこれらの高次構造はプロセスの進行につれ次第に減少していくと考えられる。
表面粗さは確率的概念なので、面全体を2次元的に測定する必要がある。縦方向の精度としては、サブnmが必要であろう。あたかも石膏型の凹凸によって原型の凹凸を知るように、酸化膜の膜厚分布を知ることによって、酸化膜とウエハーとの界面の高次構造についての情報を得ることができるかもしれない。しかし2次元エリプソメータの面内分解能は1ないし100μmのオーダーで、表面の形態に対しては非常に粗く、測定の結果は多数の微視的構造について平均化していることになるので、そこからどの程度デフィニットな情報が導き出されるだろうか。面内分解能の1単位にはおよそ100ないし10000の微視的構造が含まれる。ウエハー全体を測定することは、初期条件が少しずつ異なるこれらの微視的構造のアンサンブルにたいする、実の粗視的観察を行うことである。1)このアンサンブルの分布はウエハー固有の特性をどのようにあらわしているだろうか。
1) このことが言えるためには、1単位に含まれる微視的構造の数に比べて十分大きい数の単位を測定しなければならない。
われわれは異なる粗さ(基板のウエハーの粗さはそれぞれ0.3、0.5、1.0nmRMS)を持ったウエハー上に25nm、および50nmを想定してつけた酸化膜を2次元エリプソメータQR120K(面内分解能300μm)によって測定してみた。以下では25nmの厚さの酸化膜について説明する。
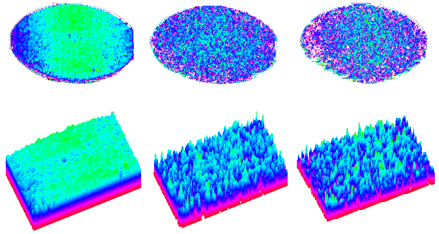
図1
膜厚25nmの酸化膜の膜厚表示。上段はウエハー全体、下段はサンプル中央部の3次元表示。基板の粗さは左からRMS0.3、0.5、1.0nm
図1は膜厚25nmの酸化膜の膜厚表示で上段はウエハー全体、下段は、サンプル中央部の3次元表示を並べたものである。色分解能は1オングストロームである (256色表示)。 基板の粗さは左からRMS0.3、0.5、1.0nmである。一見して、酸化膜の膜厚分布の平坦性はウエハーの粗さに依存することがわかる。それは当然ながら成膜においてウエハーの表面粗さが重要なファクターであることを示している。
この場合サンプルによっては、エリプソメトリイの原理的な前提である膜と基板との平行性やサンプルへのビームの一様な入射などの仮定がもはや局所的には成立しなくなってくる。そしてミクロスコピックに観測するにつれ屈折率や膜厚の測定結果には特異点が不規則にあらわれてくる。一見、測定結果が不安定に見えるこれらの特異点はサンプルそのものの不規則性を(定性的ではあるにせよ)表しているのである。2)
2) 従来の1点式のエリプソメータは、探針である光ビームの直径が大きい(約1mmφ)ことと、測定点数が少ないために、この不規則性を観測できなかった。半導体基盤技術研究会 UC標準化委員会 材料部会: ウルトラクリーンテクノロジー 5(1993)[3] 51(237)
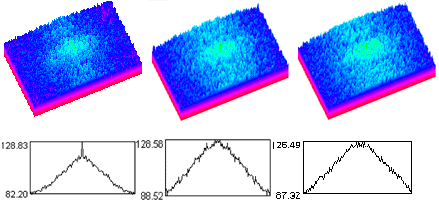
統計的解析のためにウエハーの中央部256×256ピクセルの領域の膜厚のスペクトルを計算してみた。図2はその領域全体の、図3は1-3象限のスペクトルである。(グラフの中央部が直流成分となる光学表示)。(以下の図においてすべて、ウエハーの粗さは左から0.3、0.5、1.0nmRMS)。図2のスペクトルの標準偏差は左からそれぞれ、17.22、19.18、20.10である。ウエハーの粗さが増すにつれ高周波成分が大きくなっていくのが見られる。
図2
ウエハーの中央部256×256ピクセルの領域の膜厚のスペクトル

図3
ウエハーの中央部256×256ピクセルの領域の膜厚の1-3象限のスペクトル
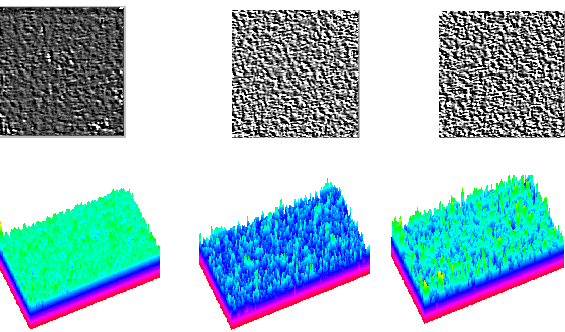
図4A
図2のスペクトルから低周波成分を取り除いた逆変換によって再生した膜厚。
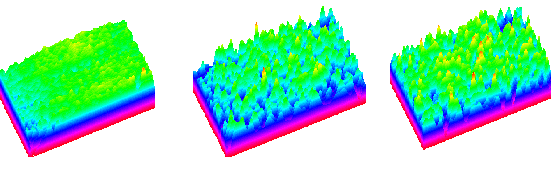
図4B
図2のスペクトルから高周波成分を取り除いた逆変換によって再生した膜厚。
粗視化によって失われた情報は大量の統計的データを集めることによって取り戻すことができる。図1で見たように、膜厚は基板の形状因子(粗さ、平坦度など)によって影響されるので、単純な膜厚分布ではなく周波数領域の分布を取ることが有効である。注目する形状因子に相当する周波数範囲をスペクトルから切り出したフーリエ逆変換によって膜厚を再生することは、しばしば有効な分析手法になる。図4Aは低周波成分を取り除いて膜厚を再生したものであり、膜厚の不規則性がよりはっきり表現されている。いっぽう図4Bは高周波成分を取り除いて膜厚を再生したものである。おのおのが同じ色で表示されていることから判るように,基板の粗さに依存しない膜厚の平均値を測定することができる。このようにしてもなお残る不規則性は入射角の一様性などの諸前提が成り立たない異常な測定点と解釈される。
スペクトルの直流成分はプロセスに対して外から設定された値である膜厚の平均値に相当し、高周波成分はプロセスの初期条件としてのウエハーの粗さに依存する。通常注目され実際的にはもっぱら測定されてきた膜厚の平均値ではなく、それ以外のゆらぎ成分にこそプロセスとサンプルの固有の特性が含まれているのである。
以上の解析とは逆に、スペクトルの低周波成分はどのような因子に依存しているだろうか。ほぼ同じ粗さ(RMS0.3nm)のウエハーを、GF3R(Global Front 3Points Range)とGBIR(Global Back-side Ideal Range)とがそれぞれほぼ同じ平坦度をあらわすようにグループ分けして膜付けしてみた。図5は25nmの酸化膜をつけた測定値の代表的な結果で、膜厚を3次元表示したものである。ウエハーの平坦度の代表的な値は左からTTVで1.0、1.5、2.0μmである。図6はFFTによる膜厚のスペクトルを表示したものである。この場合は直流成分近傍でのスペクトルの形を注目すべきで、平坦度の悪いサンプルほど直流成分近傍が広い(すなわちQが小さい)ように見える。図7は直流成分近傍のみ残してフーリエ逆変換を行った結果である。

図5
膜厚25nmの酸化膜。ウエハーの粗さはRMS0.3nm平坦度は左からTTVで1.0、1.5、2.0μm
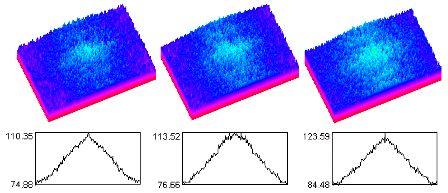
図6
図5の測定結果のスペクトル。

図7
図6のスペクトルから直流成分近傍のみ残したフーリエ逆変換によって再生した膜厚
このように2次元エリプソメータによる膜厚測定の数学的解析は、ウエハーの表面粗さの解析(そしてそれが成膜過程でどのように影響していくか)にとって興味深い手段を提供する。そこでは、どの範囲のスペクトルに注目して膜を再生するかは解析者の判断にゆだねられていて、その選択に応じて測定結果は異なる姿をあらわす。この作業をつうじて(通常の1点式の測定では捨てられていたのであるが)、プロセスとサンプルにかかわる固有の貴重な情報を汲み出すことができる。
これらの解析の定量的な結論は主に装置の面内分解能に依存している。ユーレカはより細かい面内分解能をもった装置を開発中であるので、それによってさらにこのテーマを追及していく予定である。
|